- Attila Bérczes (University of Debrecen) – VIDEO
On some diophantine equations in separated variables
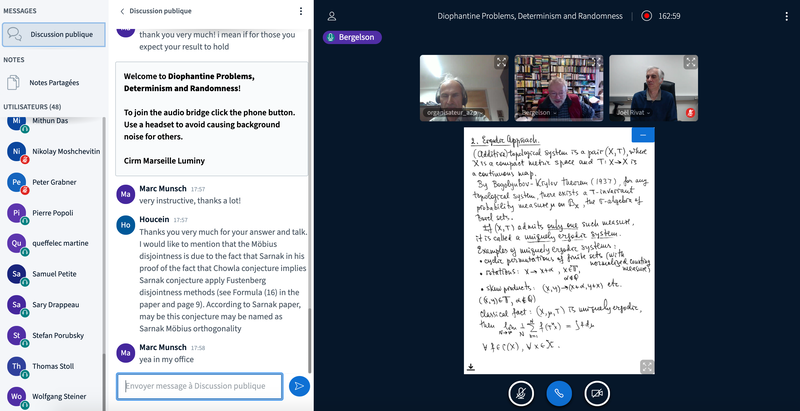
- Vitaly Bergelson (Ohio State University) – VIDEO
Independence of actions of (N,+) and (N,×) and Sarnak’s Möbius disjointness
- Régis de la Bretèche (IMJ-PRG Paris) – VIDEO
Higher moments of primes in intervals and in arithmetic progressions, II
- Jörg Bruedern (Georg-August-Universität Göttingen)
Bracketed ternary additive problems
- Cécile Dartyge (Université de Lorraine) – VIDEO
The Rudin-Shapiro function in finite fields
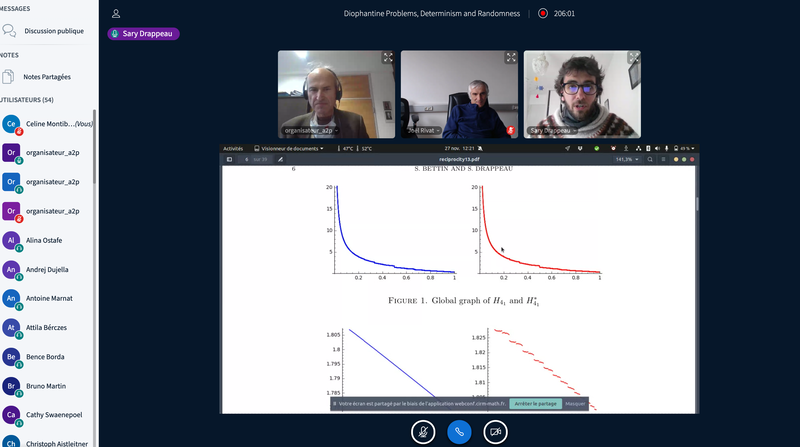
- Sary Drappeau (Aix-Marseille Université) – VIDEO
Modularity of the q-Pochhammer symbol and application
- Michael Drmota (TU Wien) – VIDEO
(Logarithmic) densities for automatic sequences along primes and squares
- Andrej Dujella (University of Zagreb) – VIDEO
D(n)-sets with square elements
- Christian Elsholtz (TU Graz) – VIDEO
Improved cap constructions, and sets without arithmetic progressions
- Daniel Fiorilli (Université Paris-Saclay)
Higher moments of primes in intervals and in arithmetic progressions, I
- Christopher Frei (TU Graz) – VIDEO
Constructing abelian extensions with prescribed norms
- Kalman Györy (University of Debrecen) – VIDEO
Effective finiteness results for diophantine equations over finitely generated domains
- Philipp Habegger (University of Basel) – VIDEO
Equidistribution of roots of unity and the Mahler measure
- Lajos Hajdu (University of Debrecen) – VIDEO
Skolem’s conjecture and exponential Diophantine equations
- Florian Luca (University of the Witwatersrand) – VIDEO
Fibonacci numbers and repdigits
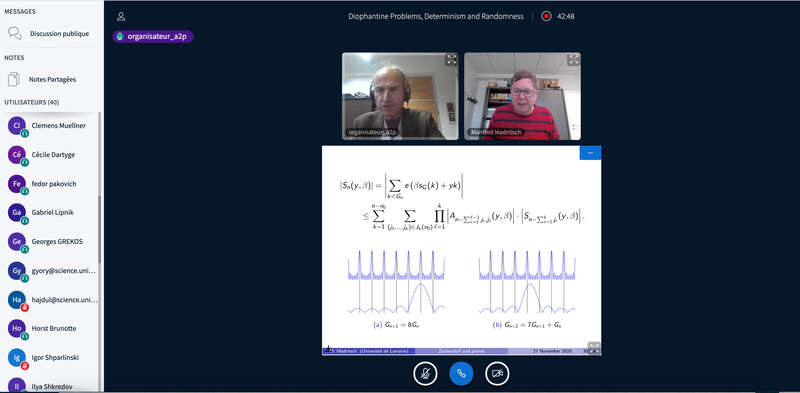
- Manfred Madritsch (Université de Lorraine) – VIDEO
The sum-of-digits function in linearly recurrent number systems and almost primes
|
- Bruno Martin (Université de la Côte d’Opale) – VIDEO
Some interactions between number theory and multifractal analysis
- Nikolay Moshchevitin (Lomonosov Moscow State Univ.)
Diophantine exponents, best approximation and badly approximable numbers – VIDEO
- Alina Ostafe (UNSW Sydney) – VIDEO
Dynamical irreducibility of polynomials modulo primes
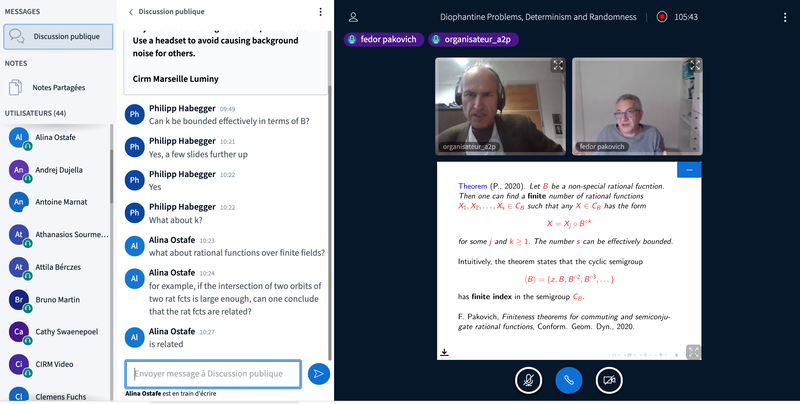
- Fedor Pakovich (Ben Gourion University of the Negev)
On amenable semigroups of rational functions
- Fabien Pazuki (University of Copenhagen) – VIDEO
Bertini and Northcott
- István Pink (University of Debrecen) – VIDEO
Number of solutions to a special type of unit equations in two unknowns
- János Pintz (Alfréd Rényi Institute Budapest) – VIDEO
Large values of the remainder term of the prime number theorem
- Ilya Shkredov (Steklov Mathematical Institute) – VIDEO
Zaremba’s conjecture and growth in groups
- Igor Shparlinski (UNSW Sydney) – VIDEO
Pseudorandomness at prime times and digits of Mersenne numbers
- Thomas Stoll (Université de Lorraine) – VIDEO
On generalised Rudin-Shapiro sequences
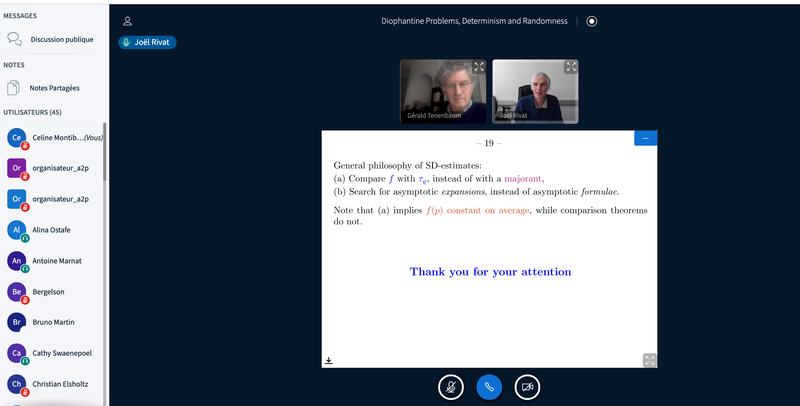
- Gérald Tenenbaum (Université de Lorraine)
Recent progress on the Selberg-Delange method in analytic number theory
- Jörg Thuswaldner (Montanuniversität Leoben) – VIDEO
Multidimensional continued fractions and symbolic codings of toral translations
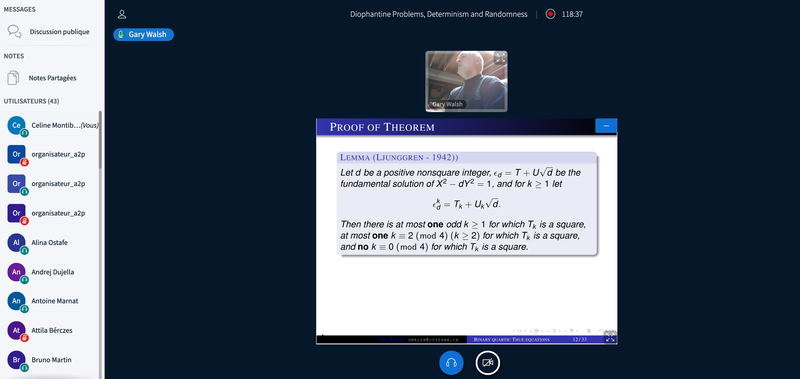
- (PG) Gary Walsh (University of Ottawa) – VIDEO
On binary quartic Thue equations and related topics
- Barak Weiss (Tel Aviv University) – VIDEO
Classification and statistics of cut-and-project sets
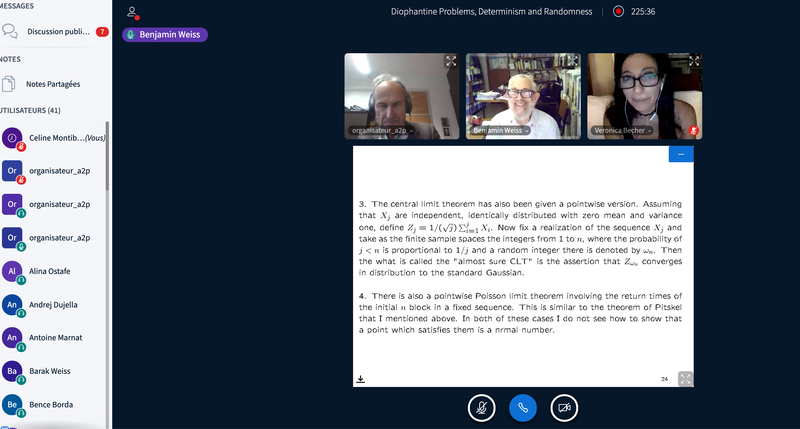
- Benjamin Weiss (Einstein Institute of Mathematics)
Poisson-generic points – VIDEO
- Volker Ziegler (Paris-Lodron University Salzburg)
On S-Diophantine Tuples – VIDEO
|